HELP FILE
FOR: DESIGN PROGRAM FOR SPREADER BARS
WITH LUGS TOP AND BOTTOM:
DEFINITION:
This program can be used to design spreader bars fabricated from structural members such as pipe, square tube or beams (beams that are non-compact/compact with their lengths less than Lu). It is left to the user to verify that any beam selected meets the non-compact, compact and Lu criteria as presented in the appendix below. These are spreader bars that have two lugs located above the structural member and two or more lugs located below the structural member. It is also applicable to spreader bars where the CG of the load does not hang under the center of the bar. In this case, the CG will be located on a point on the bar that is defined by a vertical plumb line that runs down from the hook thru the CG of the load. Again, this is not necessarily the center of the bar.
This program can also be used to design spreader bars that have the top lug holes located on the centerline of the bar, ie, Versa Bars, etc. In this case, set the vertical distance from the centerline of the bar to the centerline of the top lug holes to zero.
PROGRAM OBJECTIVE:
The objective of this program is to help the spreader bar designer develop a design that is efficient and safe. It can also be used to check the design of an existing spreader bar. The output information conforms to the requirements of AISC and ASME B30.20. The program also provides the tensions for the lifting slings and their lengths, i.e., the rigging hook up.
Refer to the examples at the end of this help file for design tips.
PRE-DESIGNED LIFTING LUG DETAILS:
Details for pre-designed lifting lugs can be found by clicking on the “Lug “ button on the input/output screen of the program.
WHAT THE PROGRAM DOES NOT DO:
This program does not design the lifting lugs or size the welds to connect the lugs to the spreader bar. The lugs and welds must be designed using one of the “lug design” programs in the same design section of this website. One lug program designs pad eye type lifting lugs and the other one designs plate type lifting lugs.
It is recommended that the lugs be
designed before the spreader bar is designed so that the distance from the
centerline of the top lugs to the centerline of the spreader bar will be known. Otherwise, a conservative guess will have to
be made and latter verified. See Quiz
26 for a sample lug design.


It is recommended that lifting lugs similar to the ones shown in the elevation view, the sketch above or the photo be used. By slotting the pipe, square tube or beam flanges, the lugs can be inserted into the slots and welded on with fillet welds. Usually a fillet weld smaller than the thickness of the pipe wall, square tube wall or the flange/web of the beam can be used, which will be much smaller than butt welds required to attach the same capacity pad eye lugs. Attaching the lugs in this fashion is much safer than using pad eye lugs with butt welds.
Note the dashed lines in the sketch above, which indicate lines of force from the slings. When these lines meet at the centerline of the spreader bar, there is zero moment in the spreader bar due to the influence of the slings.
Note that there are two top lugs in the photo, one on either side of the beam web
ASME B30.20 requires that all spreader bars be marked with the Manufacturer’s name, the serial number of the bar, the weight of the bar and the rated load. It is recommended that the rated load be based on a specific sling angle and that sling angle be listed as the fifth item on the tag.
UNITS CONVERSIONS:
To convert from kips to metric tons (Te), divide the kips by 2.2046
To convert from pound/feet to kg/m, multiply the lb/feet by 1.4882
To convert from kip-in. to Te-cm, multiply the kip-in. by 1.1521
To convert from ksi to Te/cm^2, divide the ksi by 14.2231
To convert from inches to centimeters, multiply the inches by 2.54
To convert from in^2 to cm^2, multiply the in^2 by 6.45
To convert from in^3 to cm^3, multiply the in^3 by 16.39
To convert from in^4 to cm^4, multiply the in^4 by 41.62
TOTAL LOAD:
The total load is the combined weight of the load and any items that might be included for erection, i.e., trays, insulation, piping, platforms & ladders, fire proofing, weight contingency, rigging, etc. It is input as either kips (1 kip = 1,000 lbs.) or metric tons (Te).
ANGLE OF THE LEFT SLING:
When the CG of the load does not hang under the center of the spreader bar, different lengths of slings must be used to keep the hook centered over the CG. Use the smaller of the two sling angles for the input value for the left sling. It is recommended that all sling angles be kept at 60 degrees or greater. The program will calculate the angle of the right sling.
HORIZONTAL DISTANCE, BEARING TO BEARING
ON DUPLEX CRANE HOOK.
This horizontal distance is measured from the center of the bearing area on one prong to the center of the other prong. If a load block with a single hook is being used, enter zero for this value. See the elevation view of the spreader bar and rigging.
LENGTH OF THE SPREADER BAR, overall:
The overall length of the spreader bar is measured from one end of the spreader bar to the other end. This distance is only used in figuring the bending in the spreader bar due to its own weight.
STRUCTURAL MEMBERS:
In using this program, only the following structural shapes can be used as the main horizontal member for a spreader bar:
a. Pipe
b. Square tubing
c. Beams, non-compact or compact whose lengths are less than Lu. It is left to the user to determine if the beam being considered is non-compact or compact and its length is less than Lu. See explanation of Lu in appendix below
The properties of some structural shapes are included in the lookup table in the program. The user can select a structural shape and the properties will be imported into the appropriate fields of the program.
Note: The Lu of the beams listed in the lookup table is based on a Yield Stress (Fy) of 36 ksi. See Lu below on how to treat Lu for a 50 ksi beam.
If a structural shape is not listed that the user would like to consider, then the user can click on the SHAPES button, input the shape description, for example “Beam W12x64”, and then input its properties directly into the fields of the program. The American Institute of Steel Construction (AISC) lists all available shapes and their ENGLISH units. For structural shapes with properties listed in METRIC units, the user will have to refer to other sources.
RADIUS OF
GYRATION (r):
For beams, use the radius of gyration for the weak axis, i.e. ry for the y-y axis.
EFFECTIVE
LENGTH FACTOR (K):
The program uses an effective length factor of 1.0 for spreader bar design.
MODULUS OF ELASTICITY:
The program uses a modulus of elasticity of 29,000 ksi or 2,038.94 Te/cm^2 for spreader bar design.
IMPACT FACTOR:
A minimum impact factor of 1.80 should be used for new design in order to conform to ASME B30.20, which limits stresses to .33*Fy. By using 1.80, the allowable stresses can be used as printed in the AISC Manual.
The program allows a variable impact factor to be used so that when checking an existing design, the impact factor can be determined that was used to calculate the stated allowable load for the spreader bar. If the impact factor turns out to be less than 1.8, the program user will then have to make a decision as to the structural integrity of the spreader bar based on the actual impact factor, its application and the risk involved.
The impact factor is limited to 1.25 or greater. If an impact factor less than 1.25 is used, the program shows “error” in all of the output fields and a message is displayed stating that the impact factor is less than 1.25.
The impact factor is included in the output value for the combined stress check. It is not included in any other output values.
Lu: (For Beams Only)
The program checks Lu against the distance between the top lugs and against the distance between the bottom lugs. The program considers the largest of these distances the length of the spreader bar, not the overall length. If Lu is less than either of these distances, the program shows “error” in all of the output fields and a message is displayed showing the length compared and asks the user to select a beam with a larger Lu.
For the beams in the lookup table, Lu is based on a Yield Stress (Fy) of 36 ksi. If the program user wants to use a 50-ksi beam, the properties in the look up table are still applicable. The user only needs to enter the correct Lu for 50 ksi, and change the Fy field to read 50 ksi, i.e., for a W18 x 119, Lu = 29.1’ for Fy = 36 ksi, but Lu = 21.0’ for Fy = 50 ksi.
DISTANCE FROM THE CG TO THE TOP LEFT LUG FOR ZERO MOMENT
DUE TO ANGLE OF TOP LEFT SLING:
The program calculates this
distance by using the left sling angle entered and it can be used to locate the
left top lug. The user can input the
distance back in to the program so that the extended line of the sling angle
will intersect the horizontal centerline of the spreader bar above the vertical
centerline of the lower left lug, thus ensuring that there is zero moment in
the spreader bar from the influence of the sling.
DISTANCE FROM THE CG TO THE TOP RIGHT LUG FOR ZERO MOMENT
DUE TO ANGLE OF TOP RIGHT SLING:
The program calculates this
distance by using the right sling angle and it can be used to locate the top
right lug. The user can input it back in
to the program so that the extended line of the sling angle will intersect the
horizontal centerline of the spreader bar above the vertical centerline of the
lower right lug, thus ensuring that there is zero moment in the spreader bar
from the influence of the sling.
KL/R:
The program uses a slenderness ratio (kl/r) equal to a maximum of 120. If this maximum is exceeded, “error” will show in all of the output fields. A message will be displayed that asks the user to increase the member size in order to reduce the kl/r down below 120.
The length of the spreader bar (l) used to calculate kl/r is the distance between the top lug holes or the distance between the bottom lug holes, which ever is the greater distance.
MOMENT DUE TO THE COMPRESSIVE FORCE IN THE SPREADER BAR
AND THE OFFSET OF THE TOP LUGS:
This moment can be negative or positive. A negative value indicated that the spreader bar is being bowed up at the centerline. The user can use this negative value to good use by balancing out the positive moments of the other bending moments, so that the net bending moment can be zero or slightly negative. This provides the maximum capacity for the spreader bar. See examples 2 & 4.
A negative moment occurs when the sling angles are higher than the ones that cause zero bending moment in the spreader bar.
NET BENDING MOMENT IN THE BAR:
The net bending moment can also be
negative or positive for the same reason as given above.
AXIAL AND BENDING
STRESSES:
The program checks the actual axial stress (fa) against the allowable axial stress (Fa). If fa > Fa, then “error” will show in all of the output fields. A message is displayed, asking the user to reduce this stress. It makes the same check for the bending stress.
COMBINED STRESS CHECK:
The combined stress check is the governing factor concerning the allowable capacity of the spreader bar. This value must always be less than 1.0. If it is greater than 1.0, the program will show “error” in all of the output fields. There are several ways that this value can be lowered. The load can be reduced, the angle of the lift slings can be increased, the location of the top lugs can be changed, or a member with a larger cross-section can be chosen. Sometimes a combination of the above might be used.
For a given run, if the combined stress check is slightly greater than 1.0 and the output fields all show ERROR, it is recommended that the input value of the load be reduced until ERROR is no longer displayed in the output fields. The user can then look at the output values and decide if the location of the lugs should be relocated per the first two output fields, if the angle of the slings should be increased, etc. If either of the above are implemented and the combined stress check drops below 1.0, then the input value of the load can be increased until the combined stress check is equal to 1.0. See example two below.
EXAMPLE 1: Using the program with English Units.
The “sample values” button at the
bottom of the screen contains input for a typical spreader bar problem. By clicking on “sample values” the input
values are shown with the output values blank.
By then clicking on “calculate”, both the input
and output values are shown. See
Rigging Quiz # 26 for a lug design using the sample values above.
EXAMPLE 2: Using the program with English Units.
Use the same input values as in Example 1. Go to the output values for the “Distance from the top left lug to the CG” and the “Distance from the top right lug to the CG” and note that they are respectively 168.94 inches and 149.71 inches. Enter these values for the same dimensions back into the input section and note that the moment due to the compression force changes from 215.37 kip-in. to 14.78 kip-in. and the combined stress check changes from 0.92 to 0.71.
Next change the angle of the left sling from 68 degrees to 69 degrees and note that the moment due to the compression force changes to –77.58 kip-in. and the combined stress check changes to 0.58. The negative –77.58 indicates that the spreader bar is being bowed up in the center and this moment is counteracting the moment due to the weight of the spreader bar. The net moment is now 21.16 kip-in.
Now change the pipe size from a 18 x 0.375 wall to a 14 x 0.375 wall and note that the combined stress is 0.80. Therefore, a pipe size of 14 x 0.375 would also work after fine-tuning the design per the above two paragraphs.
Now change the pipe size back to an 18x0.375 and increase the impact factor (I.F.) to 3.05 and note that the combined stress check is 0.99. This means that the design of the bar is based on 650 kips * 3.05 = 1982.50 kips.
Another way to look at it is to change the impact factor back to 1.8 and increase the load to 1,100 kips and note that the combined stress check is 0.99. An increase in load capacity of 1,100/650 = 169 %. This increase is based on the 1.8 impact factor. 1.69*1.8 = approx. 3.05
EXAMPLE 3: Using the program with Metric Units.
The “sample values” button at the bottom of the screen contains input for a typical spreader bar problem. By clicking on “sample values” the input values are shown with the output values blank. By then clicking on “calculate”, both the input and output values are shown.
EXAMPLE 4: Using the program with Metric Units.
Use the same input values as in Example 3. Go to the output values for the “Distance from the top left lug to the CG” and the “Distance from the top right lug to the CG” and note that they are respectively 429.11 cm and 380.26 cm. Enter these values for the same dimensions back into the input section and note that the moment due to the compression force changes from 248.14 Te-cm to 16.88 Te-cm and the combined stress check changes from 0.92 to 0.71.
Next change the angle of the left sling from 68 degrees to 69 degrees and note that the moment due to the compression force changes to –89.53 Te-cm and the combined stress check changes to 0.58. The negative –89.53 indicates that the spreader bar is being bowed up in the center and this moment is counteracting the moment due to the weight of the spreader bar. The net moment is now 24.22 Te-cm.
Now change the pipe size from a 45.72 x 0.953 wall to a 35.56 x 0.953 wall and note that the combined stress is 0.80. Therefore, a pipe size of 35.56 x 0.953 would also work after fine-tuning the design per the above paragraph.
Now change the pipe size back to a 45.72 x 0.953 and increase the load to 498.96 Te and note that the combined stress check is 0.99. An increase in load capacity of 498.96/294.84 = 169 %
APPENDIX:
This appendix contains reference material from the American Institute of Steel Construction (AISC) giving the definition of compact beams, non-compact beams and beams with lengths equal to but not greater than Lu where Lu is the maximum unbraced length of the compression flange at which the allowable bending stress may be taken at 0.6*Fy.
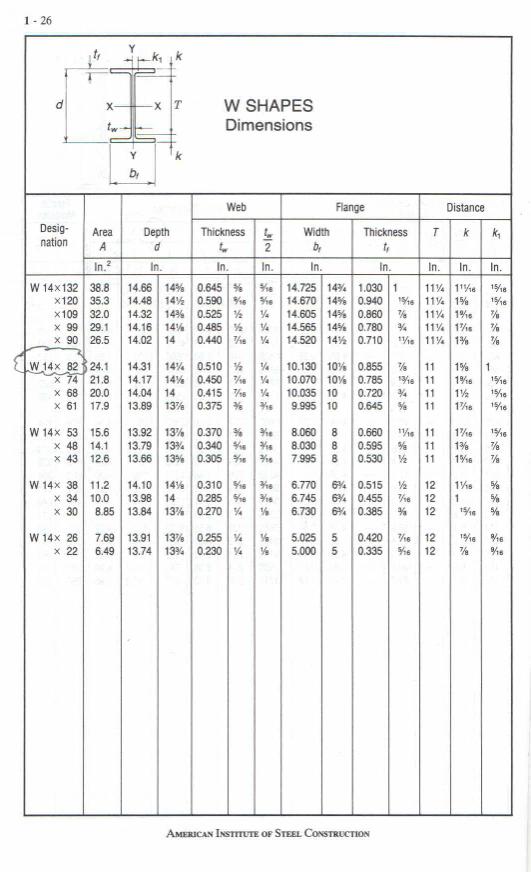
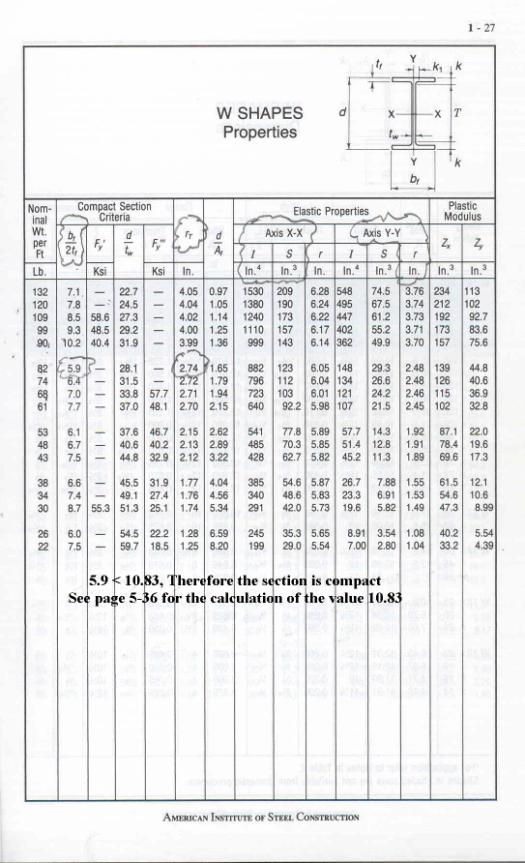
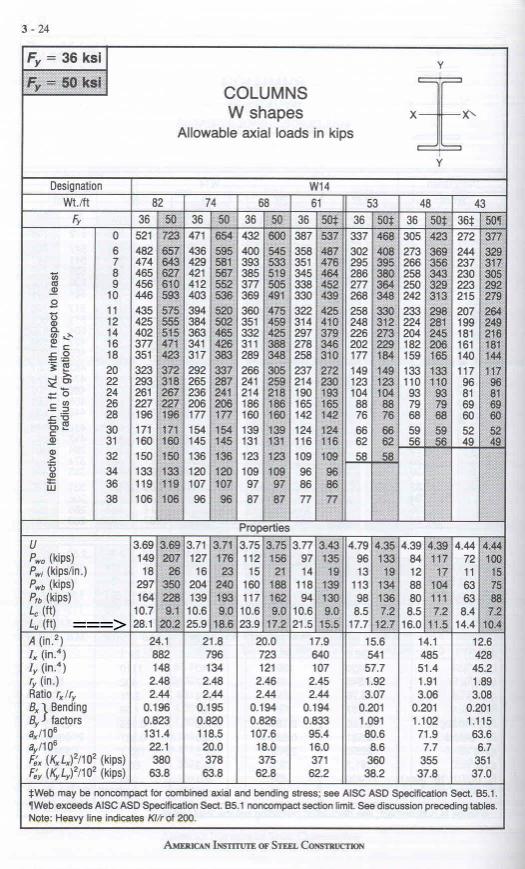
The example used is a W14 x 82 wide flange beam where:
Rt = 2.74 inches See page 1-27 below
Lu See page 2-146 for definition
Lu = 28.1 feet See page 3-24
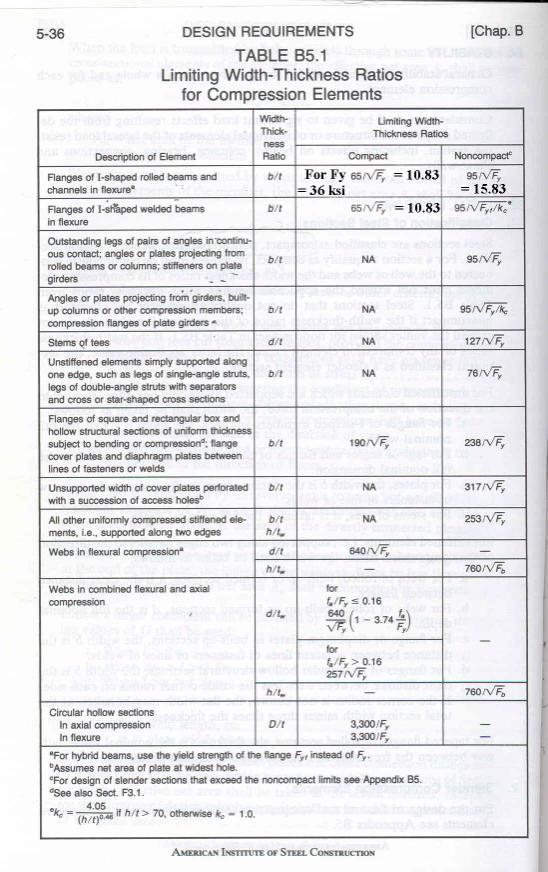
Compact beam See page 5-35 for definition
Non-compact beam See page 5-35 for definition
Limiting W/t ratios See page 5-36
Rt See page 5-47 for method of calculation
Formulas F1-6 & 8 See page 5-47
Rt See page 5-47 for definition




END OF HELP FILE